Laboratório Virtual de Física

Estudo do movimento sob ação do campo gravitacional: lançamento de projétil.

Para você refletir

Objetivos

  • Calcular o ângulo em que ocorre o alcance máximo
  • Calcular o alcance máximo
  • Calcular a altura máxima atingida pelo objeto

    • Roteiro do experimento

  • Variar a velocidade mantendo o ângulo fixo.
  • Variar o ângulo mantendo a velocidade fixa.
  • Para ambos os casos acima: qual o alcance do projétil?

    • Para determinar o ângulo em que o alcance é máximo, pode-se realizar o lançamento para diversos ângulos θ diferentes e medir os diferentes alcances. Pode-se construir um gráfico θ×A\theta\times A

    O que pode-se concluir do experimento acima?

    Explicação teórica

    Analiticamente, podemos construir uma solução para o alcance utilizando os conceitos de cinemática aprendidos no Ensino Médio: a função horária da velocidade e da posição. Podemos decompor os movimentos em horizontal, onde a aceleração é nula e, portanto, essa componente descreve um movimento retilíneo uniforme (MRU), e vertical, onde a aceleração é diferente de zero e o movimento é uniformemente variado (MUV). Primeiro, vamos encontrar uma expressão para o alcance. Como trata-se de uma medida horizontal, vamos utilizar as ferramentas do MRU:

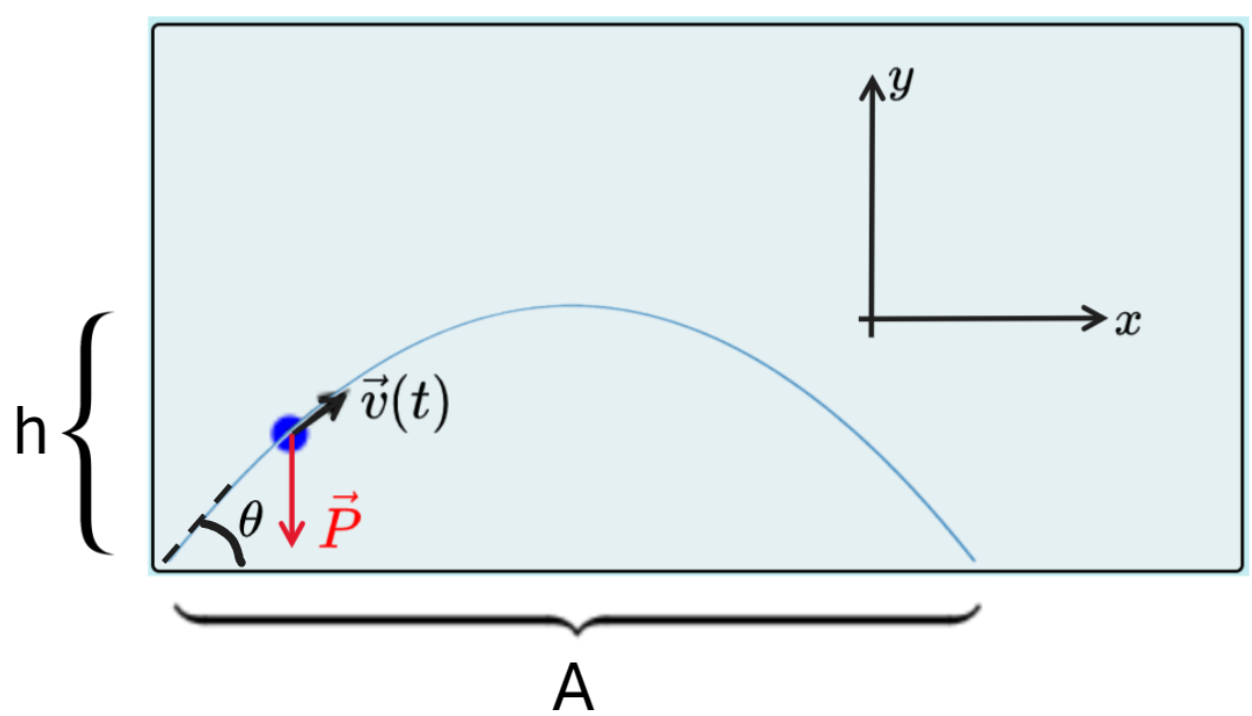
    x=x0+vxtA=0+v0Tcos⁡θA=v0Tcos⁡θ x=x_0+v_{x}t \\[3mm] A=0+v_0T\cos\theta \\[3mm] \boxed{A=v_0T\cos\theta}

    onde T é o tempo entre o lançamento e a chegada ao chão e vx=v0cos⁡θv_x=v_0\cos\theta é a componente horizontal da velocidade (que permanece constante).

    Para descobrir o alcance, portanto, precisamos do tempo de vôo T. Esse tempo é determinado pela descrição vertical do movimento. Portanto, vamos utilizar as ferramentas do MUV nessa direção:

    y=y0+v0yt+12at20=0+v0Tsin⁡θ+12aT2T(v0sin⁡θ+12aT)=0{T=0    (caso  trivial)v0sin⁡θ+12aT=0  ⇒  T=−2v0sin⁡θa y=y_0+v_{0y}t+\dfrac{1}{2}at^2 \\[3mm] 0 = 0 + v_0T\sin\theta+\dfrac{1}{2}aT^2 \\[3mm] T(v_0\sin\theta+\dfrac{1}{2}aT)=0 \\[6mm] \begin{cases} T=0 \ \ \ \ \rm (caso\; trivial) \\[3mm] v_0\sin\theta+\dfrac{1}{2}aT=0 \; \Rightarrow \; \boxed{T=-\dfrac{2v_0\sin\theta}{a}} \end{cases}

    Substituindo este resultado na expressão do alcance:

    A=v0(−2v0sin⁡θa)cos⁡θA=−v02a⋅2sin⁡θcos⁡θ⏟sin⁡(2θ)A=−v02sin⁡(2θ)a A=v_0\left(-\dfrac{2v_0\sin\theta}{a}\right)\cos\theta \\[3mm] A=-\dfrac{v_0^2}{a}\cdot \underbrace{2\sin\theta\cos\theta}_{\sin(2\theta)} \\[3mm] \boxed{A=-\dfrac{v_0^2\sin(2\theta)}{a}}

    Apesar de tanto o alcance como o tempo de percurso estar com o sinal negativo, o que não parece condizer com a realidade, mas a seguir veremos que o sinal da aceleração será negativo, fazendo com que tanto o tempo como o alcance tenham valores positivos, como esperado.

    Para isso, teremos que fazer a análise da dinâmica da situação e utilizar a 2ª Lei de Newton. A única força que atua no objeto é a força gravitacional (ou força peso); portanto, essa é a força resultante na partícula. Também cabe observar que temos uma expressão para a força peso próxima à superfície terrestre

    P⃗=mg⃗=m(−gy^)=−mgy^ \vec{P}=m\vec{g}=m(-g\hat{y})=-mg\hat{y}

    Vamos, então, utilizar a 2ª lei para determinar a aceleração:

    F⃗R=ma⃗P⃗=ma⃗−mgy^=ma⃗a⃗=−gy^ \begin{align*} \vec{F}_R&=m\vec{a}\\[3mm] \vec{P}&=m\vec{a}\\[3mm] -\cancel{m}g\hat{y}&=\cancel{m}\vec{a}\\[3mm] \vec{a}&=-g\hat{y} \end{align*}

    Observa-se que a componente y da aceleração é -g (enquanto a componente x é zero). Substituindo na expressão para o alcance:

    A=v02sin⁡(2θ)g \boxed{A=\dfrac{v_0^2\sin(2\theta)}{g}}

    1. Para responder ao primeiro item, precisamos verificar quando essa expressão é maximizada, ou seja, quando ela atinge o seu maior valor. Para isso, observamos que a função seno é limitada, ou seja, ela assume somente valores entre -1 e 1. No máximo, ela tem o valor 1. Para analisar o ângulo em que isso acontece, basta igualar o seno de theta a 1 e lembrar que o seno de um ângulo é igual a 1 quando o ângulo é de 90°. Assim:

      2. sin⁡(2θ)=12θ=90°θ=45° \sin(2\theta)=1 \\[3mm] 2\theta=90° \\[3mm] \boxed{\theta=45°}

    2. Consequentemente, conseguimos encontrar o alcance máximo igualando o seno a 1. Dessa forma, temos:

      3. Amax=v02g \boxed{A_{max}=\dfrac{v_0^2}{g}}

    3. Finalmente, para encontrar a altura máxima, precisamos utilizar a componente y do movimento. Para isso, vamos utilizar a função horária da posição e avaliar os pontos inicial e intermediário, este último onde o objeto atinge a altura máxima. Sabemos que esse ponto acontece na metade do caminho, tanto da trajetória quanto do tempo. Portanto, usando $t=T/2$ na função horária da posição, temos:

      4. y=y0+v0yt+12at2hmax=0+v0T2sin⁡θ−g(T2)22hmax=0+v0(2v0sin⁡θg)2sin⁡θ−g[(2v0sin⁡θg)2]22hmax=v02sin⁡2θg−v02sin⁡2θ2ghmax=v02sin⁡2θ2g y=y_0+v_{0y}t+\dfrac{1}{2}at^2\\[3mm] h_{max}=0+v_0\dfrac{T}{2}\sin\theta-\dfrac{g(\frac{T}{2})^2}{2}\\[3mm] h_{max}=0+v_0\dfrac{\left(\dfrac{\cancel{2}v_0\sin\theta}{g}\right)}{\cancel{2}}\sin\theta-\dfrac{g\left[\frac{\left(\frac{\cancel{2}v_0\sin\theta}{g}\right)}{\cancel{2}}\right]^2}{2}\\[3mm] h_{max}=\dfrac{v_0^2\sin^2\theta}{g}-\dfrac{v_0^2\sin^2\theta}{2g}\\[6mm] \boxed{h_{max}=\dfrac{v_0^2\sin^2\theta}{2g}}